Quadratzahlen und Zweierpotenzen
Was sind Quadratzahlen?
Multiplizierst du eine Zahl mit sich selbst, entsteht eine Quadratzahl. Die Rechenoperation heißt Quadrieren.
Beispiele
- 2$$*$$2 = 2² = 4
- 3$$*$$3 = 3² = 9
- 5$$*$$5 = 5² = 25
- 10$$*$$10 = 10² = 100
- 15$$*$$15 = 15² = 225
- 20$$*$$20 = 20² = 400
- 1$$*$$1 = 1² =1
Das Quadrieren ist eine Multiplikation mit zwei gleichen Faktoren.
- Addierst du 3 + 3 oder 5 + 5, so kannst du rechnen 2 · 3 oder 2 · 5.
- Addition mit zwei gleichen Summanden ist eine Multiplikation mit dem Faktor 2.
- Schreibweise: 3 + 3 = 2 · 3 = 6 und 5 + 5 = 2 · 5 = 10
Quadrate und Quadratzahlen
Das Wort „Quadrat“ kennst du doch eigentlich aus der Geometrie. Dieses Viereck, bei dem alle Seiten gleich lang sind und bei dem alle Winkel 90° sind. Was hat das mit diesen Zahlen zu tun??
Bestimme die Seitenlängen der Quadrate und die Anzahl der kleinen Quadrate innen drin:
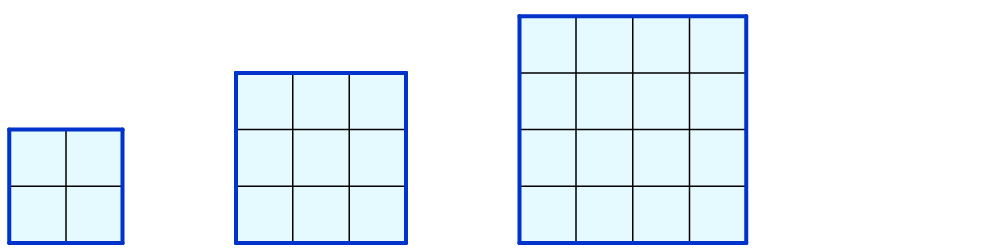
So sieht’s aus, da hast du wieder die Quadratzahlen:
| Seitenlänge | kleine Quadrate |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
Quadratzahlen des kleinen Einmaleins
Für viele Aufgaben ist es gut, wenn du die Quadratzahlen von 1 bis 10 auswendig kennst.
- 1² = 1
- 2² = 4
- 3² = 9
- 4² = 16
- 5² = 25
- 6² = 36
- 7² = 49
- 8² = 64
- 9² = 81
- 10² = 100
Kleine Eselsbrücken: „Sechs mal sechs ist sechsunddreißig, alle Kinder rechnen fleißig“. „Acht mal acht ist vierundsechzig, was du nicht lernst, das rächt sich.“
Große Quadratzahlen
Ehrlich gesagt, wird es dir auch nützen, wenn du die Quadratzahlen bis 20 weißt.
- 11² = 121
- 12² = 144
- 13² = 169
- 14² = 196
- 15² = 225
- 16² = 256
- 17² = 289
- 18² = 324
- 19² = 361
- 20² = 400
Aber natürlich kannst du auch immer ganz normal 11$$*$$11 oder 12$$*$$12 im Kopf rechnen. Dauert bloß länger.
Die „Rechentricks“ kannst du auch für große Quadratzahlen anwenden. Beispiel:
34²
= (30 + 4)² = 900 + 16 + 2 · 30 · 4
= 900 + 16 + 240 = 1156
Vom Quadrat zur Zweierpotenz
Du kannst eine Zahl nicht nur einmal mit sich multiplizieren, sondern auch mehrmals.
Wichtig ist das für die 2, für andere Zahlen erstmal nicht so.
$$2*2= 2^2 = 4$$
$$2 · 2 · 2 = 2 ^3 = 8$$ $$2 · 2 · 2 · 2 = 2 ^4 = 16$$ $$2 · 2 · 2 · 2 · 2 = 2 ^5 = 32$$ $$2 · 2 · 2 · 2 · 2 *2 = 2 ^6 = 64$$
All diese Produkte mit der Zahl 2 heißen Potenzen von 2.
Ein Produkt aus gleichen Zahlen kannst du als Potenz schreiben.
Beispiel: $$2 * 2 * 2 * 2 * 2 = 2^5$$
sprich: 2 hoch 5
kapiert.de passt zu deinem Schulbuch!
Buchreihen Mathematik mein Schulbuch suchen



